Connected components problem
Given n nodes label from 0 to n - 1 and a list of undirected edges (each edge is a pair of nodes), write a function to find the number of connected components in an undirected graph:
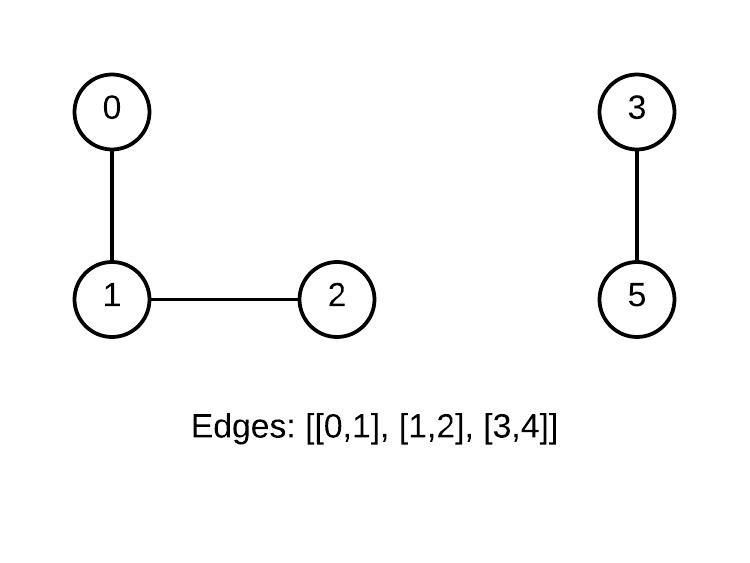
You can assume that no duplicate edges will appear in edges. Since all edges are undirected, [0,1] is the same as [1,0] and thus will not appear together in edges.
This problem can be easily be solved by a special data structure called Union Find.
Union Find Data Structure
Union Find data structure supports two operations:
- Connected(a, b): it tells you whether element
aand elementbin this graph are connected. - Union(a, b): it connected a and b.
We are able to solve the connected components problem by reusing the ideas used in Union Find data structure. Let’s first take a look how Union Find data structure is implemented.
Well, there are multiple ways to implement Union find and let’s assume We use array to represent the nodes.
Then we have to think about the following questions:
How do we know if two nodes are in one components?
We can use an array to track the components:five nodes: [0,1,2,3,4]. Then we can think of the connected components as tree and the way to check if two components are in one connected components is too look at the root of the two nodes.
private int[] id;
public void UF(int n) {
id = new int[n];
for (int i = 0; i < n; i++) {
id[i] = i;
}
}
private int root(int i) {
while (i != id[i]) {
i = id[i];
}
return i;
}
public connected(int a, int b) {
return root(a) == root(b);
}How do we connected multiple components into one?
As introduced above, we can view a connected components as a tree and the way to connected two tree is to attach the root of one tree to another tree. But we naturally have the same problem as trees: what if the tree is severely skewed, then the tree becomes a list and time complexity of tracing back to the root becomes n. And the way to solve this problem, we can use a balanced manner to construct the tree:
- Always attach the smaller tree to the larger tree.
We use another array sz[] to track the size of each tree, which is the number of nodes in each tree.
private int[] sz;
public void UF(int n) {
id = new int[n];
sz = new int[sz];
for (int i = 0; i < n; i++) {
id[i] = i;
sz[i] = 1;
}
}
}
public void union(int a, int b) {
int i = root(a);
int j = root(b);
if (i == j) {
return;
}
if (sz[i] < sz[j]) {
id[i] = j;
sz[j] += sz[i];
} else {
id[j] = i;
sz[i] += sz[j];
}
}Except for attaching one tree to another in a balanced manner, we can also do a path compression to make the tree as flat as possible. To compress the path, we only need to connect the current node to its grandparent when its parent is not root.
private int root(int i) {
while (i != id[i]) {
// connect the node to its grandparent
id[i] = id[id[i]];
i = id[i];
}
return i;
}With the data structure we have the solution to the connected components problem ready:
public int countComponents(int n, int[][] edges) {
int[] roots = new int[n];
int[] size = new int[n];
for (int i = 0; i<n; i++) {
roots[i] = i;
size[i] = 1;
}
for (int[] edge: edges) {
int root1 = find(roots, edge[0]);
int root2 = find(roots, edge[1]);
if (root1 != root2) {
// union in a balanced manner
if (size[root1]<size[root2]) {
roots[root1] = root2;
size[root2] += size[root1];
} else {
roots[root1] = root2;
size[root1] += size[root2];
}
n--;
}
}
return n;
}
public int find(int[] roots, int id) {
while (roots[id] != id) {
// path compression: connect to the grandparent.
roots[id] = roots[root[id]];
id = roots[id];
}
return id;
}