Dynamic Programming: Maximal Rectangle

Maximal Rectangle problem

Given a 2D binary matrix filled with 0’s and 1’s, find the largest rectangle containing only 1’s and return its area.

For example, given the following matrix:

1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0

Return 6.

Height, left boundary and right boundary

A rectangle within a matrix can be decided by three dimensions:

• Height of the rectangle: counts the number of successive ‘1’s above (plus the current one)
• left/right boundary: the boundaries of the rectangle which contains the current point with a height of value height

If you look at the following square, you will find that we can find three different square:

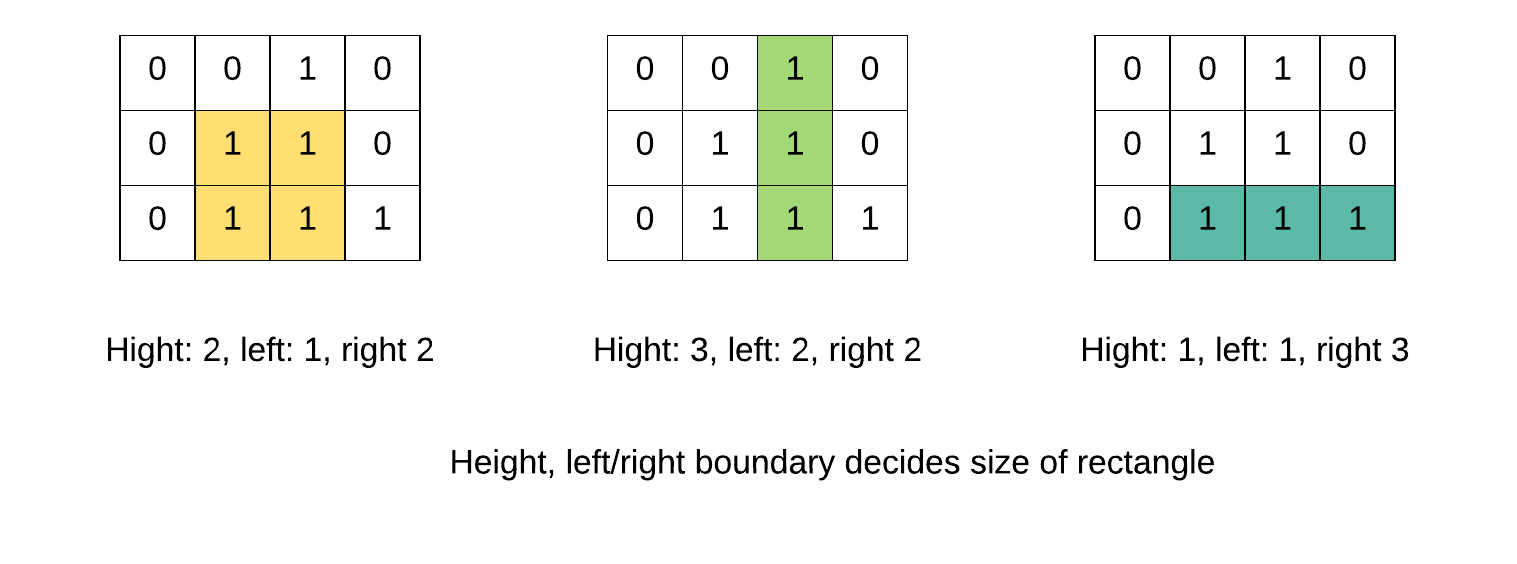
• rectangle 1: height 2, left boundary index 1, right boundary index 2
• rectangle 2: height 3, left boundary index 2, right boundary index 2
• rectangle 3: height 1, left boundary index 1, right boundary index 3

Correctness

The question is:

How does this algorithm guarantees find maximal rectangle ending at bottom row.

If we only take a look at the example, it is based on the following truth:

• Rectangle 1 is the largest rectangle with height of 2
• Rectangle 2 is the largest rectangle with height of 3
• rectangle 3 is the largest rectangle with height of 1
  Then the rectangle with the largest area must be in one of them.

Reduction Transition Function

The next question is:

what will happen if we add another row?

In the following diagram, one more row is added.

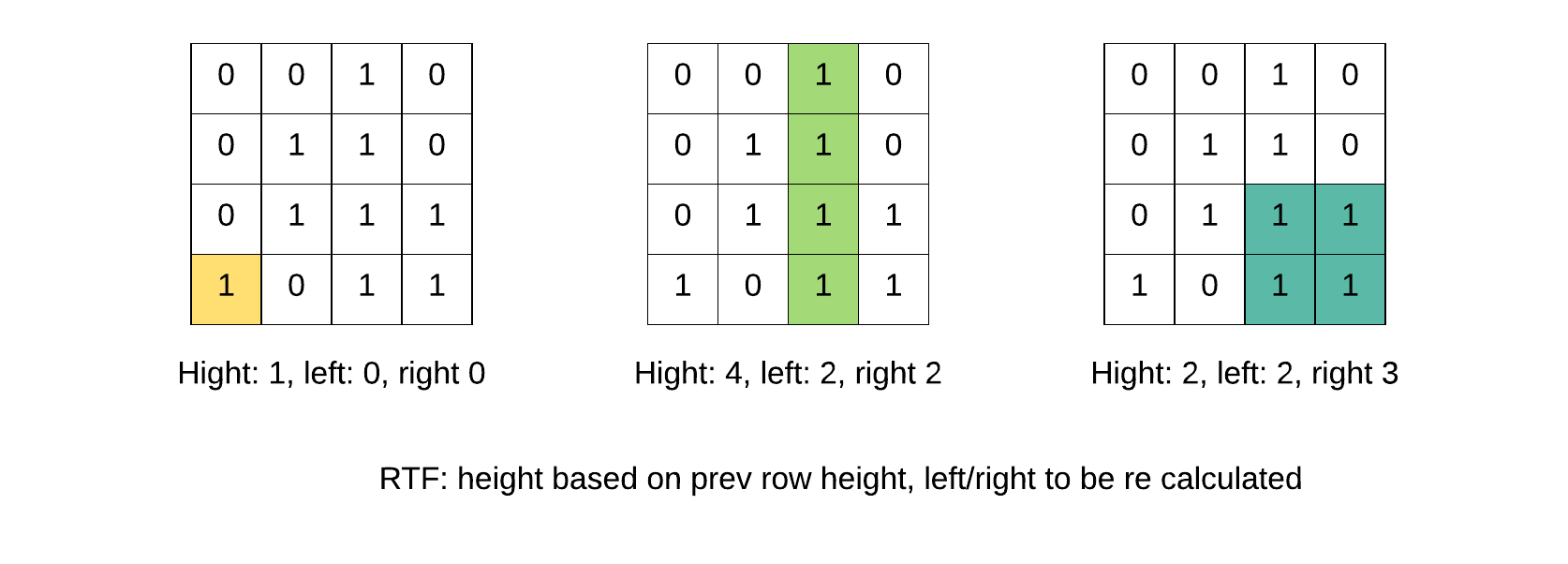
Three new square if formed when this new row added, the height/left boundary/right boundary have to be recalculated.

Height RTF:

• height[i][j] = matrix[i][j] == ‘1’ ? height[i – 1][j] + 1 : 0

Left boundary RTF:

• currleft = matrix[i][j] == ‘1’ ? currleft : j + 1
• left[i][j] = matrix[i][j] == ‘1’ ? max(left[i – 1][j], curr_left) : 0

The following diagram illustrate how this transition works:

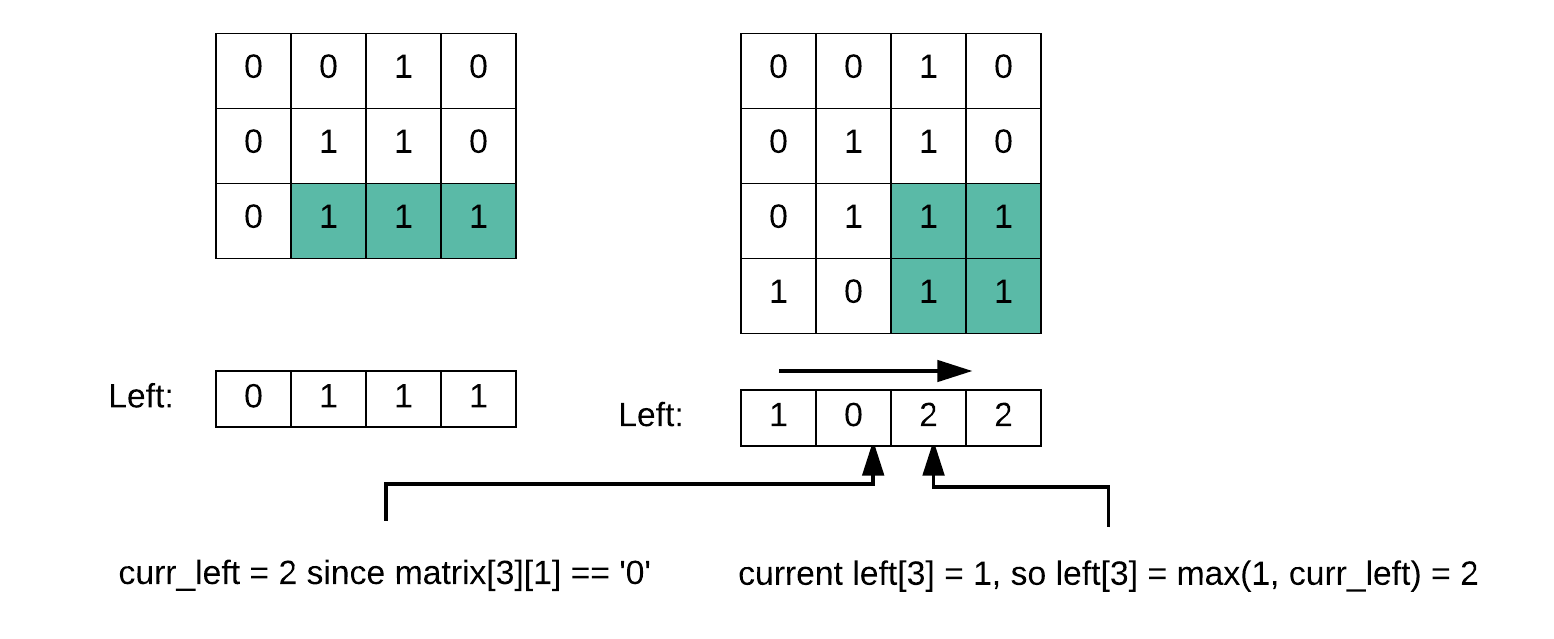
• curr_left = 0
• matrix[3][1] = ‘0’ => curr_left = j + 1 = 2
• matrix[3][2] = ‘1’ => left[1] = max(left[3], curr_left) = 2

We need to update curr_left because when previous cell is ‘0’, previous column could not be counted, hast to restart.

Let’s change matrix[3][1] to ‘1’:

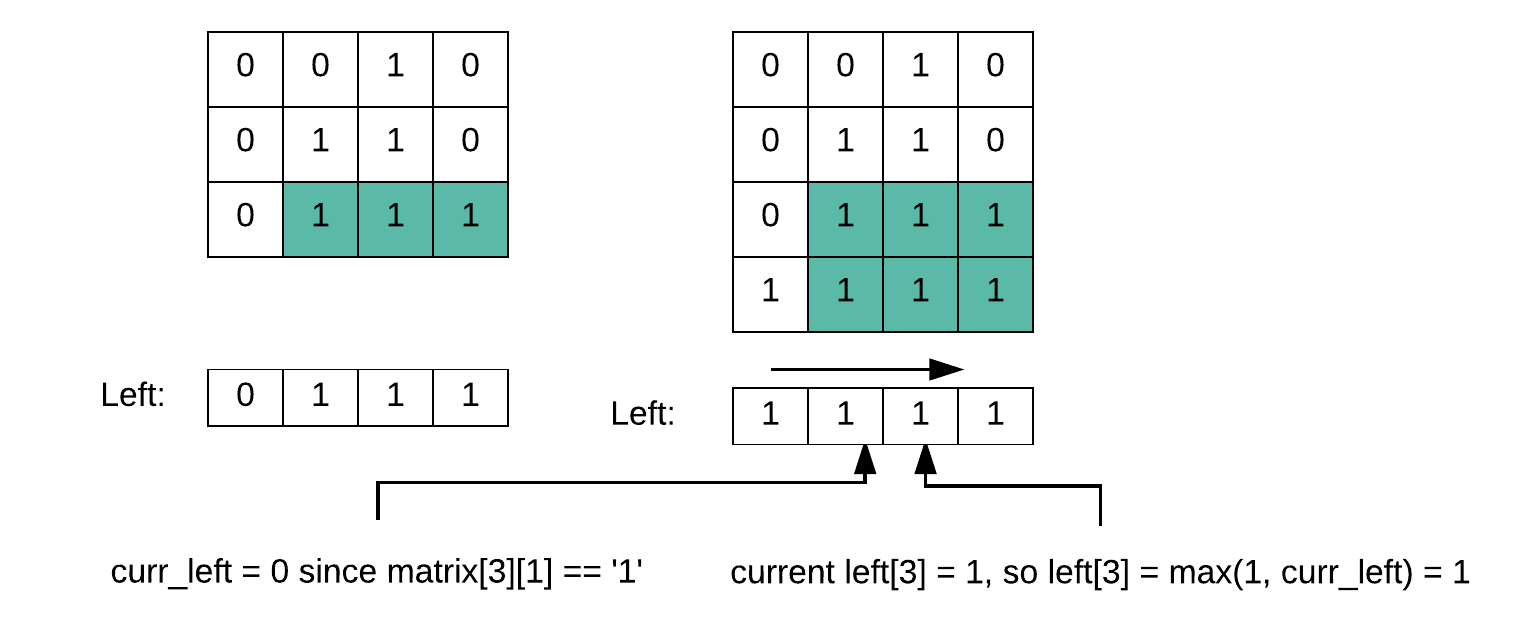
• curr_left = 0
• matrix[3][1] = ‘1’, left[2] = max(0, left[2]) = 1
• matrix[3][2] = ‘1’, left[3] = max(1, left[3]) = 1

When previous cell is ‘1’, previous column could sill be counted, no need to restart.

Right boundary RTF:

• currright = matrix[i][j] == ‘1’ ? currright : j
• right[i][j] = matrix[i][j] == ‘1’ ? min(right[i – 1][j], curr_right) : n;

This is the same as we construct left boundary.

Implementation

We can use a rolling array to replace the matrix. The following is the implementation of the matrix.

public int maximalRectangle(char[][] matrix) {
    if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
        return 0;
    }

    int nrow = matrix.length;
    int ncol = matrix[0].length;

    int[] height = new int[ncol];
    int[] left = new int[ncol];
    int[] right = new int[ncol];
    Arrays.fill(right, ncol);
    int maxArea = 0;

    for (int i = 0; i < nrow; i++) {
        int currLeft = 0, currRight = ncol;
        // calculate height
        for (int j = 0; j < ncol; j++) {
            height[j] = matrix[i][j] == '1' ? height[j] + 1 : 0;
        }

        // calculate left boundary: left to right
        for (int j = 0; j = 0; j--) {
            if (matrix[i][j] == '1') {
                right[j] = Math.min(right[j], currRight);
            } else {
                right[j] = ncol;
                currRight = j;
            }
        }

        // calculate max area: right bounday does not include valid column
        for (int j = 0; j < ncol; j++) {
            maxArea = Math.max((right[j] - left[j]) * height[j], maxArea);
        }
    }

    return maxArea;
}