Dynamic programming can be very challenging in that:
- It is hard to find out whether the question can be solved by dynamic programming or not.
- It is hard to figure out the correct reduction transition function.
- It is hard to implement the algorithm correctly.
Let’s take a look at one typical dynamic programming problem to understand how each step works.
Wildcard Matching Problem
Implement wildcard pattern matching with support for ‘?’ and ‘*’.
'?' Matches any single character.
'*' Matches any sequence of characters (including the empty sequence).
The matching should cover the entire input string (not partial).
The function prototype should be:
bool isMatch(const char *s, const char *p)
Some examples:
isMatch("aa","a") ? false
isMatch("aa","aa") ? true
isMatch("aaa","aa") ? false
isMatch("aa", "*") ? true
isMatch("aa", "a*") ? true
isMatch("ab", "?*") ? true
isMatch("aab", "c*a*b") ? falseDynamic Programming
We don’t know if this problem can be solved by dynamic program algorithm or not until we can find correct reduction transition.
Reduction Transition Function
A reduction transition function reduce the problem from bigger scale to smaller scale.
To find out the reduction transition function, let’s assume:
- We have string
Aand stringB - We know whether
A[0, i]and its subsequence matchesB[0, j]and its subsequence. - Can we determine whether
A[0, i + 1]matchesB[0, j + 1]. - We use
~to represents matches with.
If we use match[i][j] to represent whether A[0, i] ~ B[0, j], then we are trying to figure out match[i + 1][j + 1]. There are three different cases:
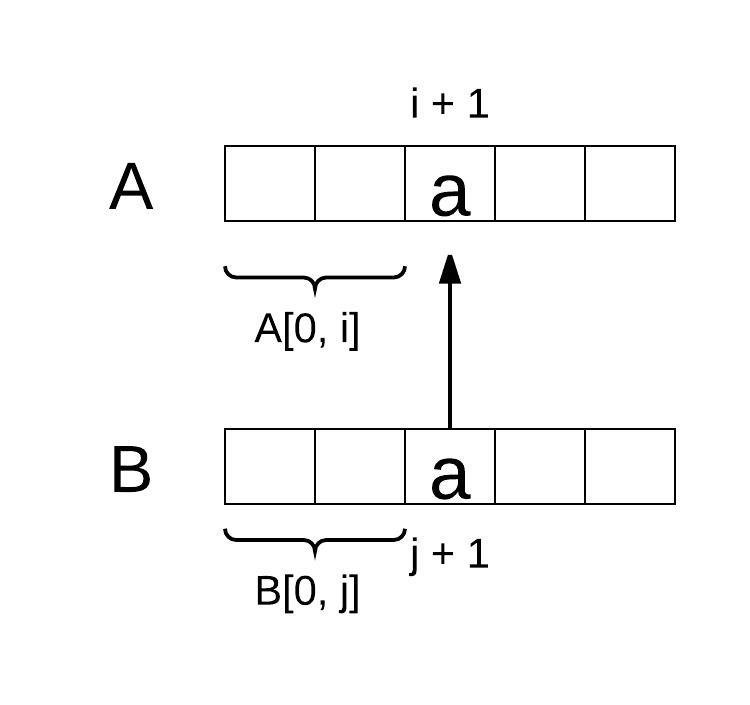
B[j] is a regular character
match[i + 1][j + 1] = match[i][j] && A[i + 1] == B[j + 1]
In this case, match[i + 1][j + 1] is determined by whether B[j] ~ A[i] and whether A[0, i] ~ B[0, j], which is match[i][j]. The following chart illustrates this case:
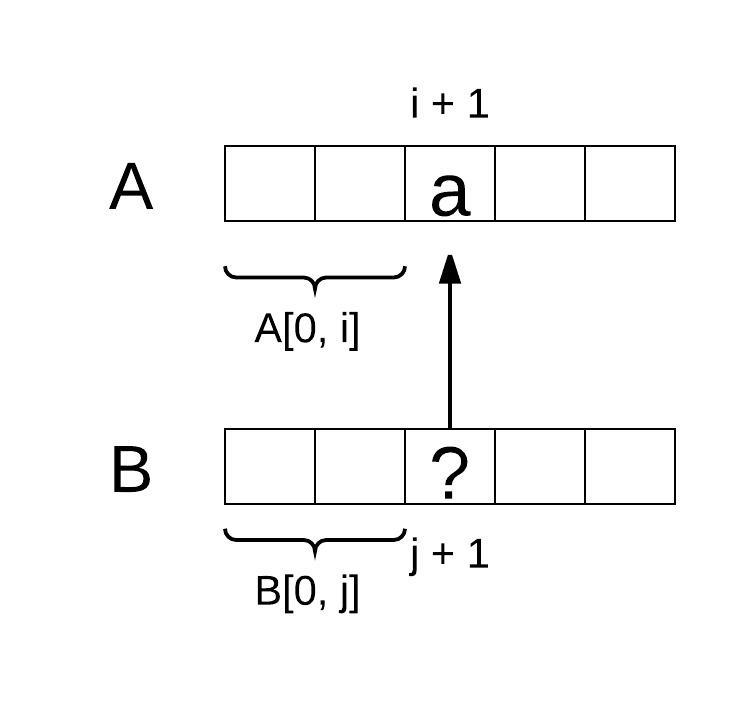
B[j] is ‘?’
match[i][j] = match[i][j]
Since ‘?’ only matches with any single character, match[j + 1][j + 1] is determined by whether match B[0, j] ~ A[0, i], which is match[i][j]. The following picture illustrates this case:
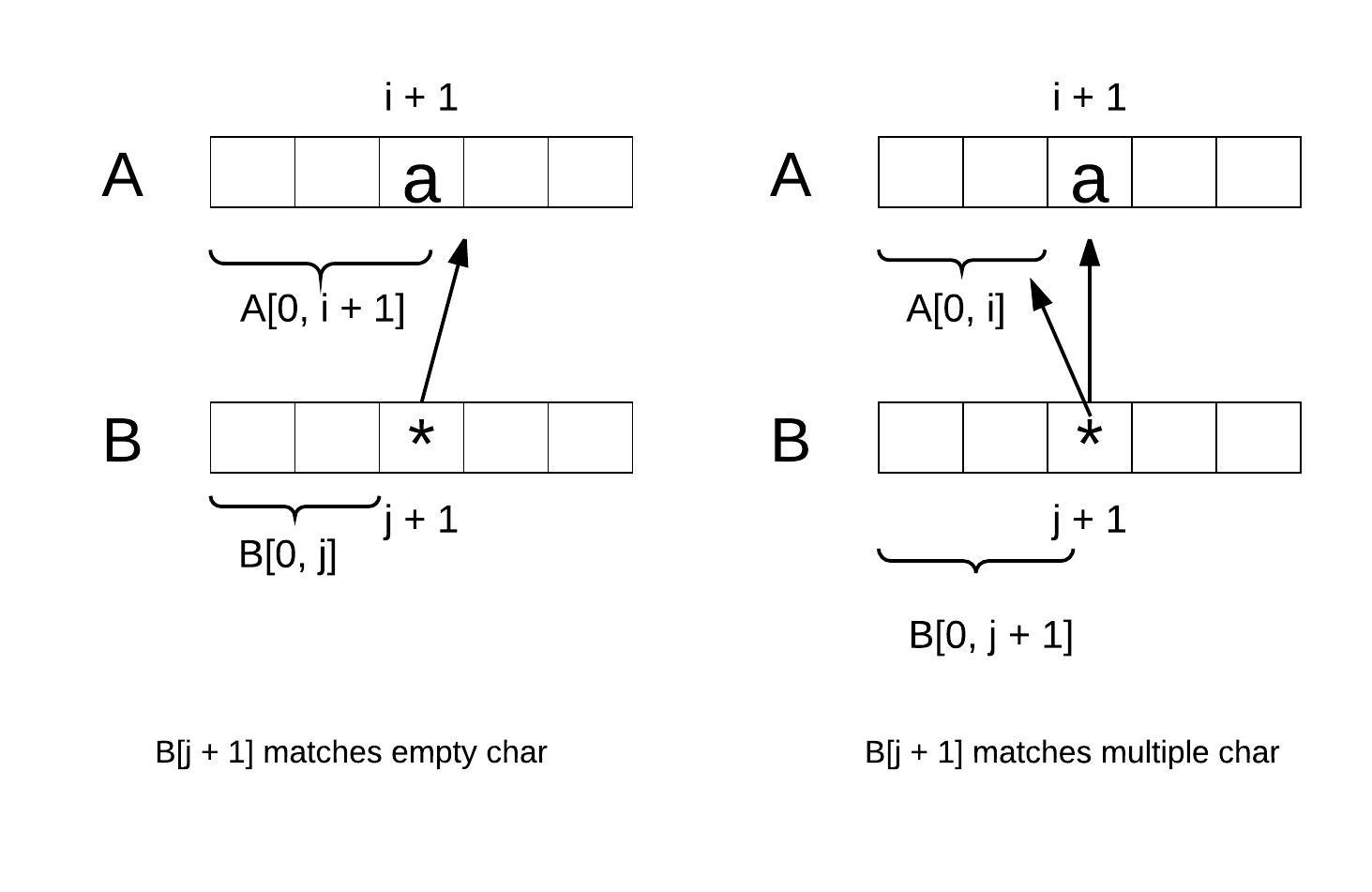
B[j] is ‘*’
match[i + 1][j + 1] = match[i][j + 1] || match[i + 1][j]
‘*’ can match with any sequence or empty sequence, there are two cases:
- B[j] matches empty string: then
match[i + 1][j + 1] = match[i + 1][j]. - B[j] matches with multiple character, which means
B[j + 1]already been used to match withA[0, i], it is used to matchA[i + 1]again, thenmatch[i + 1][j + 1] = match[i][j + 1].
The following picture illustrate this case:
Implementation
We can use a matrix to track match[i][j], the following chart shows how the move on the matrix works:
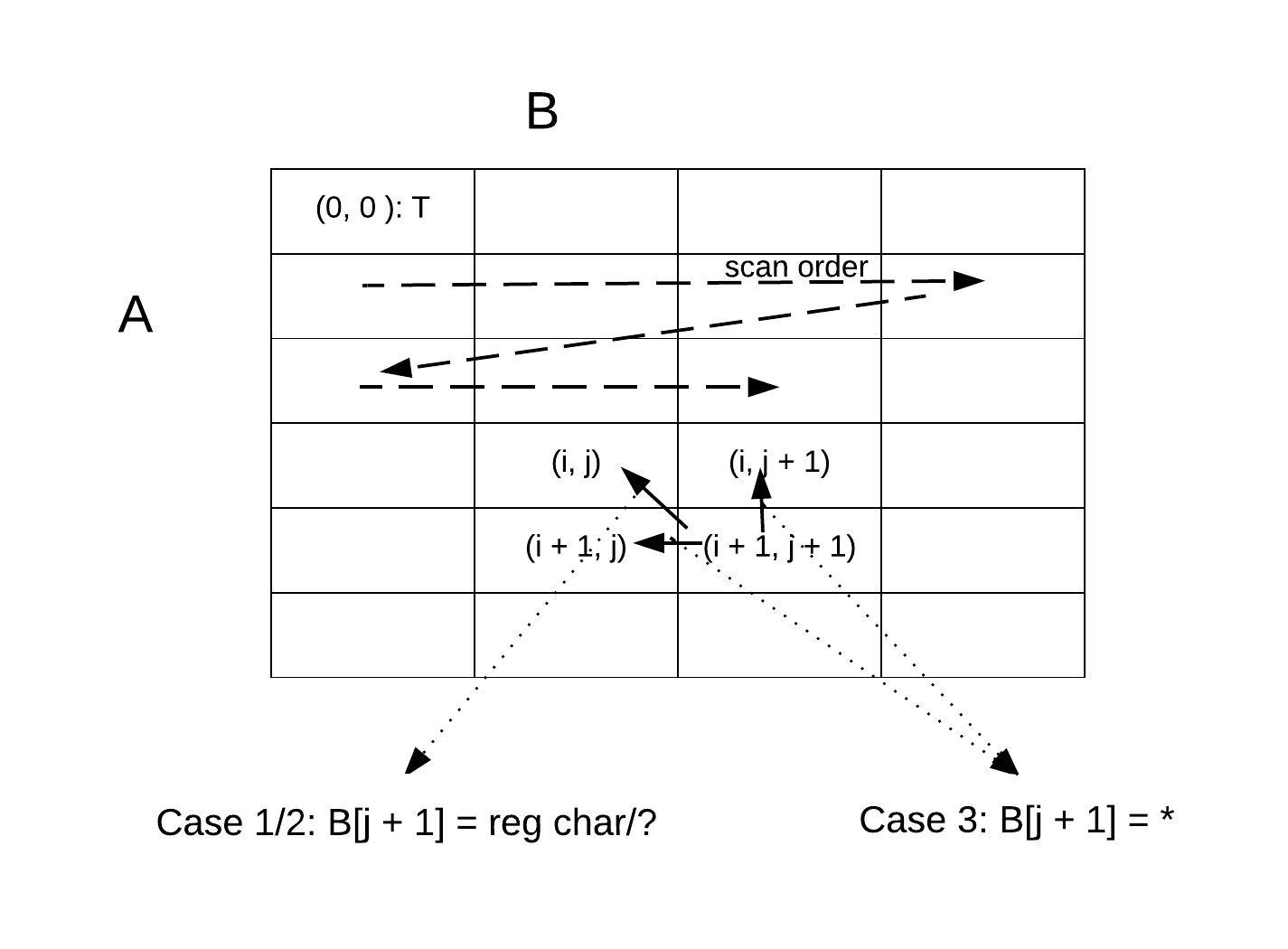
Consider that we need to look back to match[i - 1][j - 1] and match[i][j - 1]. If we only allocate match[len(A)][len(B)], when i = 0 or j = 0, we need to handle the transition separately, which makes the code verbose. So instead, we allocate matches[len(A) + 1][len(b) + 1], but we need to initiate the first row in s special way.
The following code implements the algorithm
public boolean isMatch(String s, String p) {
int len1 = s.length();
int len2 = p.length();
boolean[][] isMatch = new boolean[len1 + 1][len2 + 1];
isMatch[0][0] = true;
for (int i = 0; i<len2; i++) {
if (p.charAt(i) == '*') {
isMatch[0][i + 1] = true;
} else {
break;
}
}
for (int i = 0; i<len1; i++) {
for (int j = 0; j<len2; j++) {
if (p.charAt(j) == '?' || s.charAt(i) == p.charAt(j)) {
isMatch[i + 1][j + 1] = isMatch[i][j];
} else if (p.charAt(j) == '*') {
isMatch[i + 1][j + 1] = isMatch[i][j + 1] || isMatch[i + 1][j];
} else {
isMatch[i + 1][j + 1] = false;
}
}
}
return isMatch[len1][len2];
}Improvements
Replace the matrix with a rolling array. This can be done easily, we only need to remember a special value, which is match[i][j]. The following code implements the algorithm:
public boolean isMatch(String s, String p) {
int len1 = s.length();
int len2 = p.length();
boolean[] isMatch = new boolean[len2 + 1];
isMatch[0] = true;
for (int i = 0; i<len2; i++) {
if (p.charAt(i) == '*') {
isMatch[i + 1] = true;
} else {
break;
}
}
boolean oneCharMatch = false;
for (int i = 0; i<len1; i++) {
// update oneCharMatch
oneCharMatch = isMatch[0];
for (int j = 0; j<len2; j++) {
boolean match = false;
if (p.charAt(j) == '?' || s.charAt(i) == p.charAt(j)) {
match = oneCharMatch;
} else if (p.charAt(j) == '*') {
match = isMatch[j + 1] || isMatch[j];
}
oneCharMatch = isMatch[j + 1];
isMatch[j + 1] = match;
}
// update first char match, after first row should always set false
isMatch[0] = false;
}
return isMatch[len2];
}