Maximum Product Subarray

Maximum Product Subarray Problem

Find the contiguous subarray within an array (containing at least one number) which has the largest product.

For example, given the array [2,3,-2,4],
the contiguous subarray [2,3] has the largest product = 6.

Reduction Transition Function

Product subarray is different from sum subarray in that:

• A negative number * a negative number produce a big positive number
• A negative number * a positive number produce a small negative number
• Thus to get the localMax[i + 1], we may need to know the localMin[i]
• So we want to record the locaMax and localMin at each step.

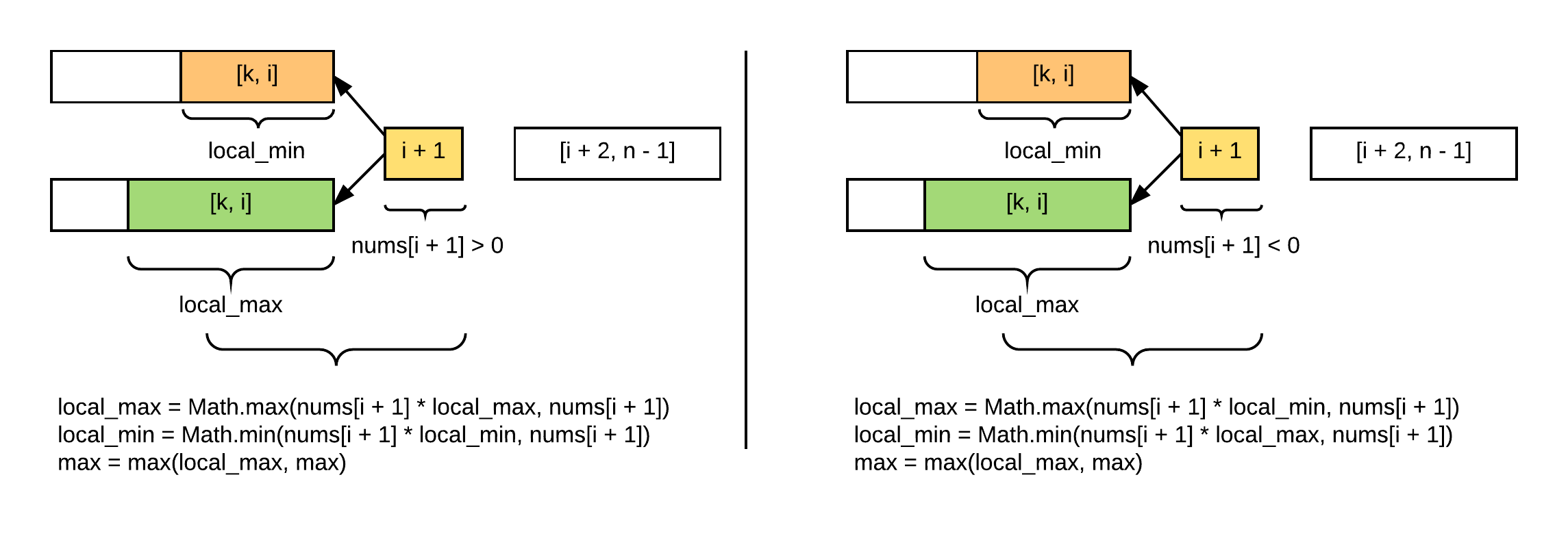
Thus we have the following RTF:

• if nums[i + 1] >= 0:
  • localMax[i + 1] = Math.max(localMax[i] * nums[i + 1], nums[i]);
  • localMin[i + 1] = Math.min(localMin[i] * nums[i + 1], nums[i]);
• if nums[i + 1] < 0:
  • localMax[i + 1] = Math.max(localMin[i] * nums[i + 1], nums[i]);
  • localMin[i + 1] = Math.min(localMax[i] * nums[i + 1], nums[i]);

The following diagram illustrates the algorithm:

Implementation

The following is the implementation of the algorithm:

public int maxProduct(int[] nums) {
    int localMax = nums[0];
    int localMin = nums[0];
    int max = nums[0];
    for (int i = 1; i < nums.length; i++) {
        if (nums[i] >= 0) {
            localMax = Math.max(nums[i], nums[i] * localMax);
            localMin = Math.min(nums[i], nums[i] * localMin);
        } else if (nums[i] < 0) {
            int localMaxTemp = Math.max(nums[i], nums[i] * localMin);
            localMin = Math.min(nums[i], nums[i] * localMax);
            localMax = localMaxTemp;
        }

        max = Math.max(localMax, max);
    }
    return max;
}

• Runtime: O(n)