Maximum Size Subarray Sum Equals K

Maximum Size subarray problem

Given an array nums and a target value k, find the maximum length of a subarray that sums to k. If there isn’t one, return 0 instead.

Note:
The sum of the entire nums array is guaranteed to fit within the 32-bit signed integer range.

Example 1:
Given nums = [1, -1, 5, -2, 3], k = 3,
return 4. (because the subarray [1, -1, 5, -2] sums to 3 and is the longest)

Example 2:
Given nums = [-2, -1, 2, 1], k = 1,
return 2. (because the subarray [-1, 2] sums to 1 and is the longest)

Algorithm

The brute force solution is straightforward, try all possible combinations:

for index i ~ (0, n):
    for index j ~ (i, n):
         if sum(i, j) == k
            minLen = min(minLen, j - i + 1);

This algorithm takes O(n ^ 2) time, which is too slow.

The second solution I thought of was a sliding window algorithm.

while (right < boundary):
    sum += nums[right++]
    while (sum == target):
        minLen = min(minLen, right - left)
        sum -= nums[left++]

Sliding window does not work for this problem because:

• Skipped part of the window may also contribute to a maxSize subarray.
• Move right does not make the sum bigger, move left does not make the sum smaller. because number can be positive or negative.

A better solution is based on the following idea:

• sum(i, j) = sum(0, j) - sum(i)
• sum(0, i), sum(0, j) can be computed incrementally

The following diagram better illustrate the idea:

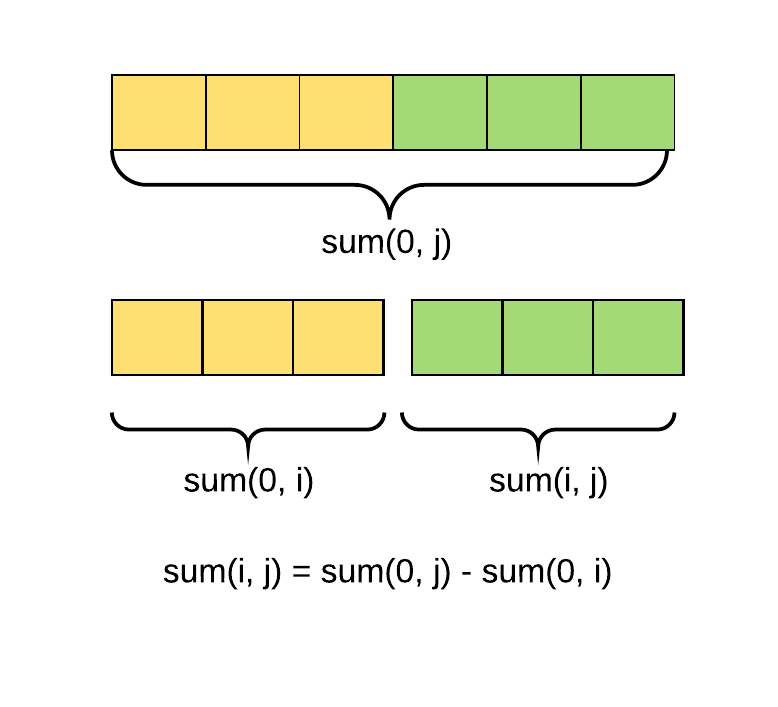
So we have the following algorithm:

for i ~ (0, n):
    sum[i] = sum[i - 1] + num[i]
    gap = sum[i] - target
    if gap in map:
        maxWindow = Math.max(maxWindow, i - map(gap))

    if sum[i] not in map:
        map.put(sum[i], i)

Implementation

The following code implemented the algorithm above:

public int maxSubArrayLen(int[] nums, int k) {
    if (nums == null || nums.length == 0) {
        return 0;
    }

    int sum = 0, maxLen = 0;
    Map<Integer, Integer> sumIndex = new HashMap<Integer, Integer>();
    for (int i = 0; i < nums.length; i++) {
        sum += nums[i];
        if (sum == k) {
            maxLen = i + 1;
        } else if (sumIndex.containsKey(sum - k)) {
            maxLen = Math.max(maxLen, i - sumIndex.get(sum - k));
        }
        if (!sumIndex.containsKey(sum)) {
            sumIndex.put(sum, i);
        } // not update index because we want max sum
    }
    return maxLen;
}

• Runtime: O(n)