Maximum Subarray Problem
Find the contiguous subarray within an array (containing at least one number) which has the largest sum.
For example, given the array [-2,1,-3,4,-1,2,1,-5,4],
the contiguous subarray [4,-1,2,1] has the largest sum = 6.
Reduction Transition Function
Consider the question in the following way:
- Assume max subarray ending at nums[i] is nums[k, i]
- What about max subarray ending at nums[i + 1]
There are two options:
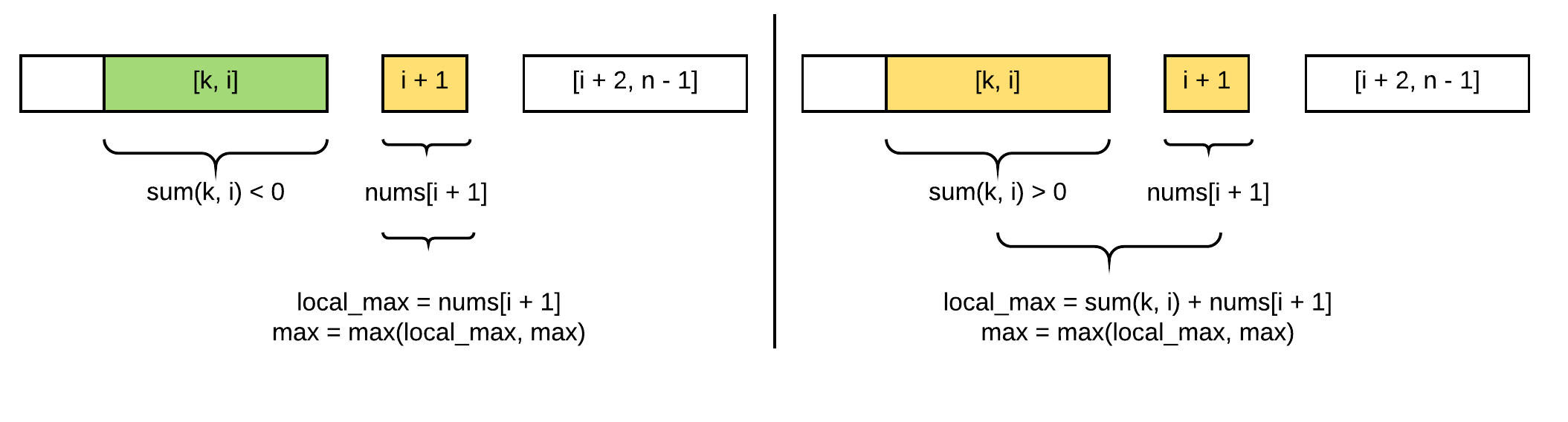
- Add nums[i + 1] into the max subarray ending at nums[i], which is nums[k, i]
- Begin anew, max subarray ending at nums[i + 1] is nums[i + 1]
We don’t need to consider adding part of nums[k, i] with nums[i + 1]. Why? Because:
- If sum(nums[k, i]) > 0, we want to add all of it
- If sum(nums[k, i]) < 0, we don’t want to add any of the element.
Thus we have the following RTF:
localMax[i + 1] = localMax[i] > 0 ? local_max[i] + nums[i + 1] : nums[i + 1]
The following diagram illustrates whether to combine nums[i + 1] with nums[k, i] or to start anew:
Then how does these localMax enable us to find the global max subarray? The following diagram illustrates the reason:
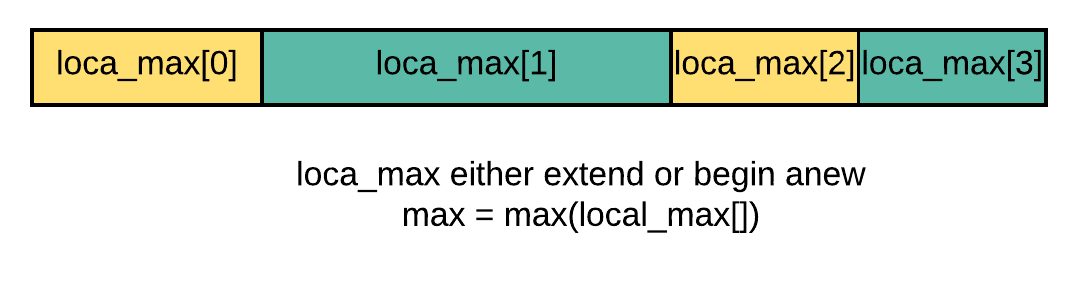
LocalMax either extend or begin anew. Thus the array is segmented by all possible localMax, and the max of them is global max, which can be proved easily.
Implementation
The following is the implementation:
public int maxSubArray(int[] nums) {
int max = Integer.MIN_VALUE, subMax = 0;
for (int num : nums) {
subMax = subMax > 0 ? subMax + num: num;
max = Math.max(max, subMax);
}
return max;
}